ピタゴラスの定理（三平方の定理）の証明

今回は、中学校で習うちょっと難しいピタゴラスの定理の証明について解説していきたいと思う。

ピタゴラスの定理は、別名、「三平方の定理」と呼ばれており、「平方」とは、2乗（数字や文字の右上に2と書かれているもの）という意味である。

3つの平方の数から成る定理ということで、三平方の定理という名前なのである。

この定理の証明方法はたくさんあるのだが、以下に有名な証明方法を示す。

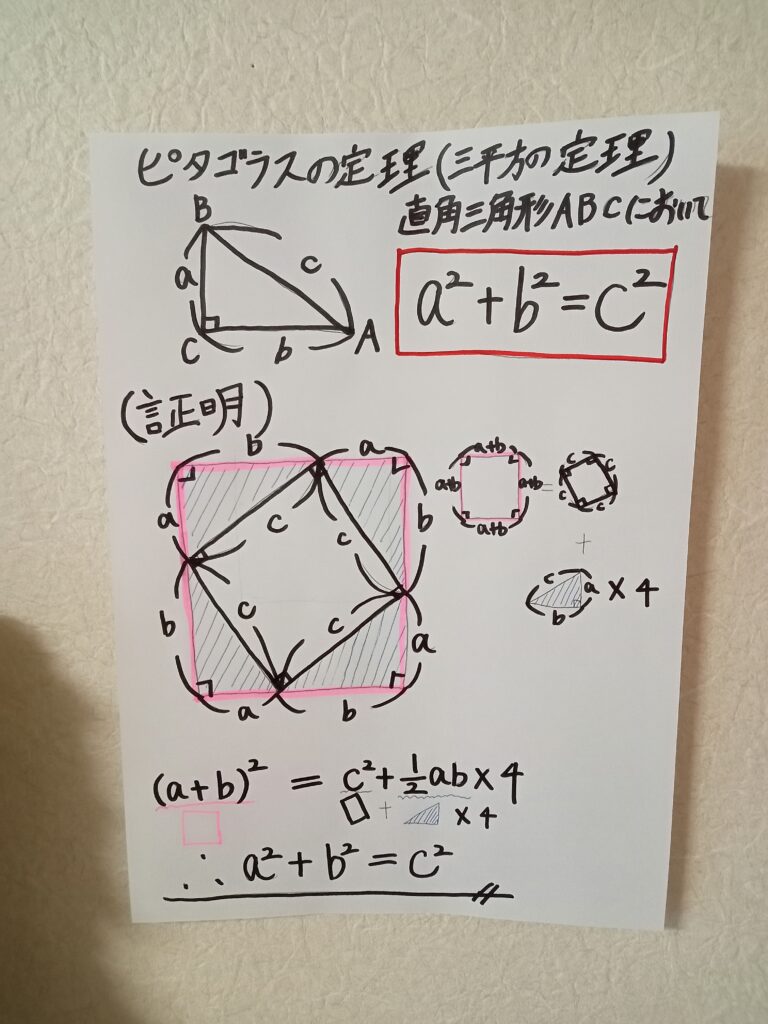
文字ばっかで何のことやらとなるかもしれないが、要するに、大きな正方形は、小さな正方形と残った三角形の4つ分を足したものに等しいということである。

文字式の計算は割愛しているが、ちゃんと計算したら出てくる。

数学では、証明をする際に、文字を置き、一般化させてどんな時でも成り立つよねといったことをする。

要するに、具体から抽象に変換させる作業が数学のメインかもしれない。

ちなみに、「∴」は、「ゆえに」ということを示す記号であり、僕は答えを書くときによく使う。

なぜなら、「∴」と「ゆえに」だったら、書くのがラクな方を選びたいからである。

また違う定理の証明も紹介していきたい。