円、正方形、正三角形のうち面積が最大なのは？

どうもビチューです。

今回は、とある数学の問題を解いてみました。

以下の通りです。

「周の長さはすべて同じであるとすると、円、正方形、正三角形のうち面積が最大なのはどれか？」

早速見ていきましょう！

それぞれの面積の値

$$ 周の長さをlとします。　$$
$$ まずは円から。　$$
$$円周率をπ,半径をr,円の面積をS_円とすると、周の長さlは、l=2πr…①$$
$$①をrについて解くと、r=\frac{l}{2π}$$
$$円の面積S_円は、πr^2なので、代入すると、$$
$$S_円=π(\frac{l}{2π})^2 =\frac{l^2}{4π} ≒ \frac{l^2}{12.56}$$
$$次は正方形。$$
$$周の長さはlなので、図形から、一辺の長さは\frac{l}{4}となるので、$$
$$正方形の面積S_4は、縦×横より、$$
$$S_4=\frac{l}{4}・\frac{l}{4}=\frac{l^2}{16}$$
$$最後に正三角形。$$
$$これも、周の長さはlなので、図形から、一辺の長さは\frac{l}{3}となります。$$
$$また、図形の性質から、θ=\frac{π}{3}なので、$$
$$三角形の面積の公式S=\frac{1}{2}absinθから、$$
$$正三角形の面積S_3は、$$
$$S_3=\frac{1}{2}・\frac{l}{3}・\frac{l}{3}・sin\frac{π}{3}=\frac{\sqrt{3}l^2}{36}≒\frac{1.73l^2}{36}$$
$$以上より、S_円>S_4>S_3となったので、円が一番面積が大きいことがわかりました。$$

正n角形の面積

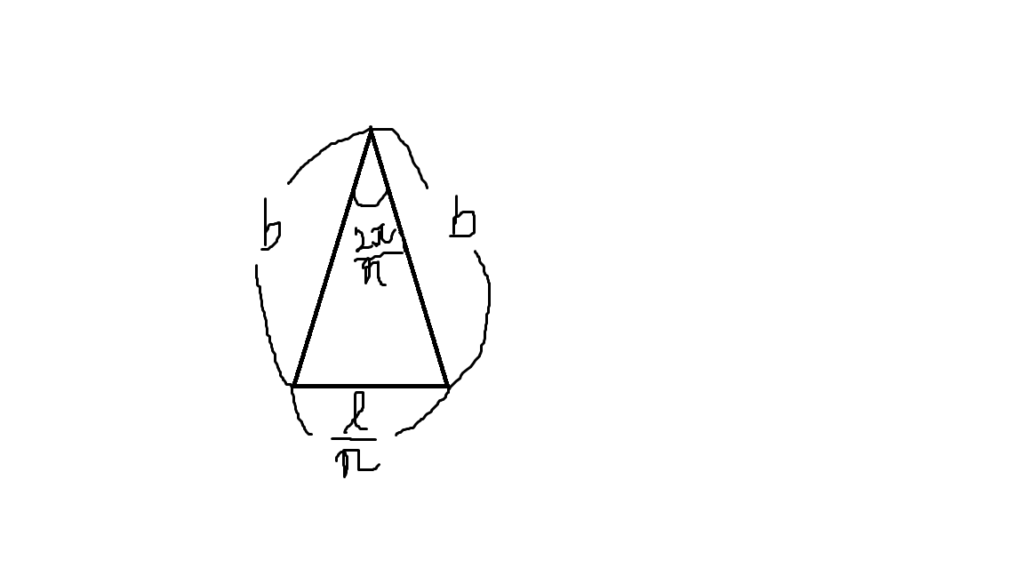
$$ついでに、周の長さがlのときの面積S_nについても考えてみました。$$
$$上図の二等辺三角形がn個合わせれば、面積S_nになります。$$
$$なので、この三角形について考えると、余弦定理より、$$
$$(\frac{l}{n})^2=b^2+b^2-2・b・b・cos\frac{2π}{n}$$
$$b^2=\frac{1}{2(1-cos\frac{2π}{n})}(\frac{l}{n})^2$$
$$よって、S_n=\frac{1}{2}b^2sin\frac{2π}{n}×n=\frac{1}{2}・\frac{1}{2(1-cos\frac{2π}{n})}(\frac{l}{n})^2・sin\frac{2π}{n}×n$$
$$=\frac{l^2sin\frac{2π}{n}}{4n(1-cos\frac{2π}{n})}$$
$$これで、S_nがわかりました。$$
$$ここで、S_nのnを∞に飛ばせば、S_円になると思うのですが、導出がわからない状態です。$$
$$まあ、ここまで解けたので、個人的にはちょっとだけ満足です笑$$