どうもビチューです。
0.999…の…は前にある数字の9がずっと続く、つまり無限に続くことを表します。
これがまさかの1と一緒つまり、1=0.999…とイコールで結べるのはなぜなのでしょうか?
私が初めてこの式を見たとき、なんとなく9が無限に続くので、感覚的には1と一緒でもういいんじゃない?という理由で納得してました。
この記事を読むことで、この何とも言えない不思議な等式が成り立つ理由が明らかになります。
中学校で習う範囲で証明できますので、早速見ていきましょう。
1を9等分にして考える。
電卓で計算してみると分かりますが、1/9は、1÷9=0.111…
同じように、2/9は、2÷9=0.222…
分数を小数で表すと、
0.111…、0.222…、0.333…、
となっているので、9/9(=1)に対応する小数は0.999…と考えられます。
だから、1=0.999…となります。
図にするとこんな感じです。
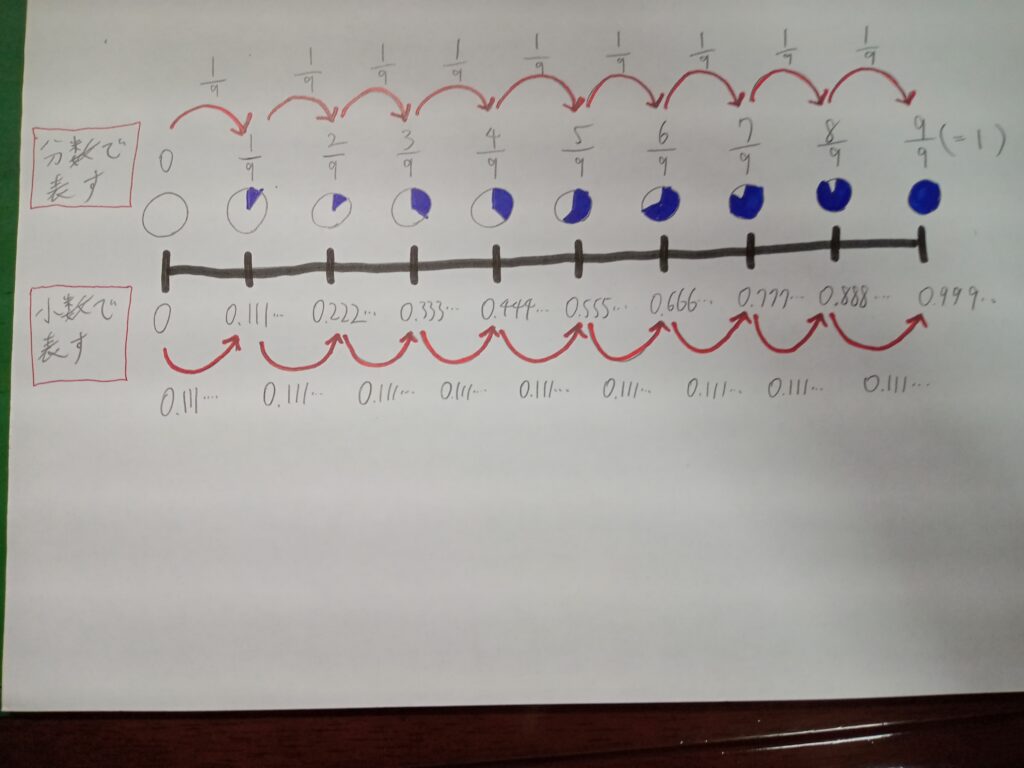
1=0.999…の証明
0.999…をxとかで置いてカッコよく証明するとこんな感じです。
x=0.999…とおく。…①
①の両辺を10倍する。
10x=9.999… …②
②ー①をする。
10xーx=9.999…ー0.999…
9x=9
両辺を9でわる。
x=1
①より、0.999…=1 となる。
まとめ
いかがだったでしょうか?
この証明がわかると、だいぶすっきりとした感覚に私はなりました。
他にも面白証明があれば、紹介していきたいと思います。


コメント